Um gráfico de correlação de dispersão é uma representação visual da relação entre duas variáveis. Ele exibe pontos de dados como pontos num gráfico, com uma variável representada no eixo x e a outra no eixo y. O padrão dos pontos pode indicar a força e a direção da correlação entre as variáveis. Aqui, falaremos acerca dos gráficos de dispersão, os diferentes tipos de correlação de gráficos de dispersão e muito mais.
Neste artigo:
Parte 1: Definição de Gráficos de Dispersão
Um gráfico de dispersão, também conhecido como diagrama de dispersão, é um tipo de diagrama matemático que usa coordenadas cartesianas para exibir valores de duas variáveis de um conjunto de dados.
Os pontos de dados são exibidos como uma coleção de pontos, cada um com o valor de uma variável que determina a posição no eixo horizontal e o valor da outra variável que determina a posição no eixo vertical.
Parte 2: Diferentes Tipos de Correlação
Há diversos tipos de correlação. Tais tipos de correlação podem ser representados de forma eficaz usando gráficos de dispersão e de correlação.
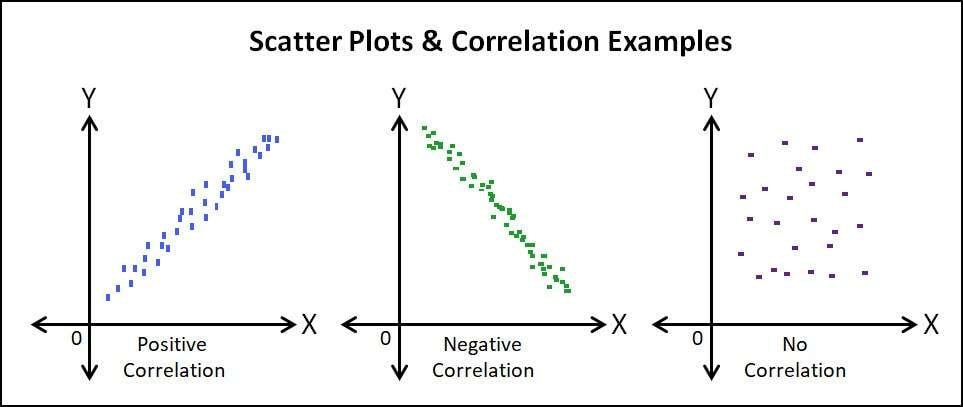
- Correlação Positiva: Uma correlação positiva existe quando os valores de uma variável aumentam à medida que os valores da outra variável também aumentam. Por outras palavras, à medida que uma variável aumenta, a outra também aumenta.
- Correlação Negativa: Uma correlação negativa ocorre quando os valores de uma variável aumentam enquanto os valores da outra diminuem. Em tal caso, à medida que uma variável aumenta, a outra diminui.
- Correlação Zero: Correlação zero, tal como o próprio nome sugere, indica que não há relação entre duas variáveis. Os valores de uma variável não afetam os valores da outra.
Parte 3: Como Você Pode Analisar a Força e a Direção da Correlação
É importante analisar a força e a direção da correlação. Seguindo algumas dicas essenciais, tal pode ser feito com eficiência.
1. Calcular o Coeficiente de Correlação:
O coeficiente de correlação, frequentemente designado por "r", é uma medida estatística que indica a força e a direção da relação entre duas variáveis. Ele varia de -1 a 1, onde -1 indica uma correlação negativa perfeita, 1 indica uma correlação positiva perfeita e 0 indica nenhuma correlação.
2. Inspeção Visual dum Gráfico de Dispersão:
Ao examinar visualmente um gráfico de dispersão, é possível ter uma ideia da direção e da força da correlação. Se os pontos no gráfico de dispersão formarem um padrão claro, tal pode indicar uma correlação forte. A direção da correlação pode ser determinada pela inclinação do padrão (positiva ou negativa).
Parte 4: Considerações a Ter ao Interpretar Coeficientes de Correlação
A interpretação de coeficientes de correlação requer algumas considerações essenciais. Tal garante que a interpretação é eficaz. A correlação de gráfico de dispersão ajuda a interpretar os coeficientes de correlação de forma mais eficaz.
- Magnitude do Coeficiente de Correlação: A magnitude do coeficiente de correlação indica a força da relação entre as variáveis. Um coeficiente próximo a 1 ou -1 sugere uma correlação forte, enquanto um coeficiente próximo a 0 sugere uma correlação fraca.
- Sinal do Coeficiente de Correlação: O sinal do coeficiente de correlação indica a direção da relação. Um coeficiente positivo indica uma correlação positiva, um coeficiente negativo indica uma correlação negativa e um coeficiente próximo de 0 indica ausência de correlação.
- Outliers e Pontos Influentes: Os outliers, ou pontos de dados distantes do restante dos dados, podem ter um impacto significativo no coeficiente de correlação. É importante identificar e avaliar a influência dos outliers na análise de correlação.
- Relações Não Lineares: O coeficiente de correlação mede a força de uma relação linear entre duas variáveis. Nos casos em que a relação é não linear, o coeficiente de correlação pode não representar a relação com precisão.
- Causalidade vs. Correlação: É crucial lembrar que correlação não implica causalidade. Mesmo que duas variáveis sejam fortemente correlacionadas, tal não significa necessariamente que mudanças numa variável causem mudanças na outra.
Parte 5: Criar um Gráfico de Correlação de Dispersão com o EdrawMax
O Wondershare EdrawMax é uma ferramenta de visualização de dados excelente e fácil de utilizar que pode ser usada para criar gráficos de correlação de dispersão.
Um gráfico de correlação de dispersão permite visualizar a relação entre duas variáveis plotando pontos num gráfico de correlação de dispersão. Além disso, a ferramenta permite personalizar os pontos de dados, linhas, legendas e muito mais para enfatizar ainda mais as relações e os padrões. Estes são os passos para criar um gráfico de correlação de dispersão usando a ferramenta:
Passo 1:
Comece por entrar na sua conta Wondershare EdrawMax. Insira as suas informações de acesso e clique no botão de entrada para acessar a plataforma.
Passo 2:
Após entrar na sua conta, localize e clique no ícone "Novo Documento" no canto superior esquerdo da interface. Isso abrirá uma tela em branco onde você poderá criar o seu gráfico de correlação de dispersão.
Passo 3:
Depois, vá para a barra lateral esquerda e selecione a opção "Modelos". Tal abrirá a galeria de modelos. Use o campo de busca para inserir "gráfico de correlação de dispersão" e pressione Enter. Escolha o modelo que melhor se adapta às suas necessidades e clique nele para o abrir.
Passo 4:
Agora, você pode alterar o modelo para corresponder às suas preferências. Personalize as fontes, cores e estilos para obter o aspecto desejado para o seu gráfico.
Passo 5:
Quando estiver contente com as alterações, salve o seu gráfico. Clique no botão "Salvar" na barra de ferramentas superior. Dê um nome ao seu gráfico e escolha se o deseja salvar no seu computador ou na nuvem.
Passo 6:
Por fim, se necessitar compartilhar ou usar o gráfico noutro sítio, exporte o gráfico do EdrawMax. Clique no botão "Exportar" na barra de ferramentas superior e selecione o tipo de arquivo que deseja para a exportação.
Conclusão
Os gráficos de dispersão facultam uma representação visual da relação entre duas variáveis, e o coeficiente de correlação quantifica a força e a direção de tal relação. É essencial compreender os diferentes tipos de correlação e de como analisar e interpretar os coeficientes de correlação para tomar decisões informadas em diversas áreas.